The Walks Mathematica Package

Mathematica Logo

Wolfram Mathematica™ is an incredibly powerful piece of software which can perform almost any kind of computation imaginable, and unsurprisingly it is very handy for performing computations on graphs. (Unfortunately Mathematica is not free, neither in the libre sense, nor in the gratis sense, but if you are a student you can probably get it for free.)

The Walks Mathematica package, in addition to various walk/CDC related commands, provides plenty of nice commands which are useful for working with matrices of graphs in general. It is very easy to download and install.

Release List

Installation and Usage Instructions

Note: If you've already installed the package and want to upgrade to a newer version, make sure you uninstall the old one first.

Download the package file from above and save it somewhere. Then open a new Mathematica notebook, go to File → Install, and you should see something like this:

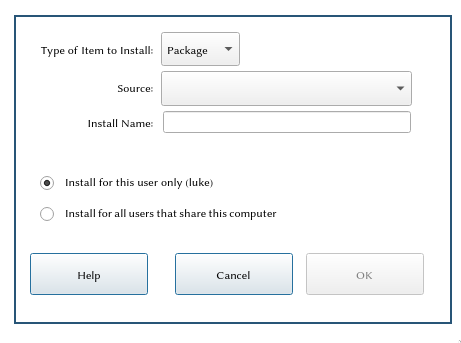
Installation screen

From the first drop down, select Package (mine already has that selected by default). For Source, select From File; at this stage you'll have to find the file you downloaded from this webpage and selected it.

The Install name should come on its own when you select the file, it should say Walks.

Then hit "OK", and exit Mathematica (don't save the notebook, just close). That's it, the installation is done!

Loading the Walks Package

If you reopen a new Mathematica notebook, type

<<"Walks`"

(note the tick ` symbol), and hit Shift + Enter, you should be able to use commands like CDC[], etc.

Command Example

To see a list of available commands, type ?Walks`*, you should be able to click on any of them to see what they do.

List of Walks Package Commands

To get information about any particular command, you can also run it with a question mark before it, and it will tell you what it does.

Example of Command Query

Please reach out if you run into any difficulties, or find any bugs!

List of Commands

Here is a list of commands and features which are included in the Walks package. As explained above, the use of the package requires first running <<"Walks`" (or Needs["Walks`"]), and information about any commands here is also available in Mathematica by typing ? followed by the command name.

Graph Arithmetic and Linear Algebra Commands

The first thing to mention isn't the addition of a command per se, but a convenient adaptation of certain Mathematica commands to be applied to graphs. For instance, usually, to obtain the eigenvalues of a graph, one would have to do

Eigenvalues[AdjacencyMatrix[g]]

and indeed, in countless situations, you would find yourself having to wrap a graph object in AdjacencyMatrix[] to do any spectral calculations. Since I do these all the time, I thought it would make life easier to redefine the commands to first check whether the object is a graph; in that case, the command makes the conversion automatically, so you can just type

Eigenvalues[g]

instead. The commands which have been adapted include: Eigenvectors, Eigenvalues, Eigensystem, Det, Tr, NullSpace, CharacteristicPolynomial, and Inverse.

In addition to linear algebra commands, I adapted the internal definition of Plus, so that it performs (disjoint) unions of graphs; thus we can do things like the following.

Addition of graphs

Subtraction also works: provided h is isomorphic to a subgraph of g, we can do g - h. Moreover, juxtaposition of graph objects gives (by default) their Cartesian product:

Product of graphs

But this can be modified using the DefaultGraphProduct[] command.

Changing the product of graphs

Commands

Here are all the commands made available by the package.

CDC[g]

This computes the canonical double cover (CDC) of the graph g.
This is equivalent to g×K2.


IsomorphicCDCQ[g,h]

This returns True if g and h have isomorphic CDCs, and false otherwise.

Note: This is not equivalent to IsomorphicGraphQ[CDC[g],CDC[h]], it is faster due to many other considerations made before the CDC is computed, so you are encouraged to use this command for speed.


WalkMatrix[g]
WalkMatrix[g,k]

This computes the walk matrix of the graph g, or the k-walk matrix if the optional integer argument k is provided.


ColourfulWalkMatrix[g]
ColourfulWalkMatrix[g,k]
ColourfulWalkMatrix[g,k,χ]

This computes the walk matrix of the graph g, or the k-walk matrix if the optional integer argument k is provided, colouring the matrix rows according to the number of walks. An optional colouring function χ:V(g)→ℕ can also be passed to it.


WalkDimension[g]

This computes the dimension of the main eigenspace of g, or equivalently, the number of columns in the walk matrix.


MainEigenvectors[g]
MainEigenvectors[m]

MainEigenvectors[g] gives a list of the main eigenvectors of the adjacency matrix corresponding to the graph object g.
MainEigenvectors[m] gives a list of the main eigenvectors of the square matrix m.
Note: An eigenvector v of a square matrix m is said to be main if it is not orthogonal to the all ones vector (1,...,1), i.e., if v.j!=0.


MainEigenvalues[g]
MainEigenvalues[m]

MainEigenvalues[g] gives a list of the main eigenvalues of the adjacency matrix corresponding to the graph object g.
MainEigenvalues[m] gives a list of the main eigenvalues of the square matrix m.
Note: An eigenvalue λ of a square matrix m is said to be main if at least one of its corresponding eigenvectors is not orthogonal to the all ones vector (1,...,1), i.e., if v.j!=0.


MainEigensystem[g]
MainEigensystem[m]

MainEigensystem[g] gives a list {values, vectors} of the main eigenvalues and eigenvectors of the adjacency matrix corresponding to the graph object g.
MainEigensystem[m] gives a list of the main eigenvalues and eigenvectors of the square matrix m.


BoldEigenvalues[g]

BoldEigenvalues[g] gives a list of the eigenvalues of the graph object or square matrix g, with main eigenvalues shown in bold. Eigenvalues which are not easily expressed as radicals are rounded to two decimal places, for nice presentation.


MainCharacteristicPolynomial[g,x]

This command gives a monic polynomial whose roots are precisely the main eigenvalues of the graph object (or adjacency matrix) g, each with multiplicity 1.


WalkPartition[g]

This function partitions the vertex set of the graph g, so that vertices in the same set have the same number of walks (of any length).


WalkColouringFunction[g]

This function associates a colour (natural number) with each vertex of the graph object g, so that vertices receiving the same colour have the same number of walks (of any length).


Colourful[g]
Colourful[g,χ]
Colourful[g,χ,options...]

Colourful[g] colours each vertex of the graph object g, so that vertices receiving the same colour have the same number of walks (of any length).
Colourful[g,χ] colours each vertex of the graph object g, according to the colouring function χ:V(g)→ℕ.

Warning: If ≥10 colours are required, the extra colours will be randomly generated and might result in similar looking colours for differently coloured vertices. In that case, run the command multiple times to be safe.


ActualColours[Assoc]

Converts a "colouring function" (i.e., association), which outputs positive integers, into a function which actually outputs RGB colours.

Warning: If ≥10 colours are required, the extra colours will be randomly generated and might result in similar looking colours for differently coloured inputs. In that case, run the command multiple times to be safe.


LabelVertices[g]

This displays the graph object g with labelled vertices.


UnlabelVertices[g]

This displays the graph object g without labelled vertices.


FreshLabels[g]

This relabels the vertices of the graph object g using positive whole numbers (1,2,…).


IsolatedVertices[g]

This returns a list of vertices in the graph object g which are isolated (i.e., have no neighbours).


IsolatedLoopedVertices[g]

This returns a list of vertices in the graph object g which are isolated and have a loop (i.e., have no neighbours apart from themselves).


IsolatedVerticesQ[g]

This returns True if g contains isolated vertices, and False otherwise.


IsolatedLoopedVerticesQ[g]

This returns True if g contains isolated vertices with a loop, and False otherwise.


RemoveIsolatedVerticesQ[g]

This returns the graph object g with any isolated vertices removed.


RemoveIsolatedLoopedVerticesQ[g]

This returns the graph object g with any looped isolated vertices removed.


AddIsolatedVertex[g]
AddIsolatedVertex[g,k]

This returns the graph object g with an isolated vertex added, or if the optional argument k is given, then it returns the graph with k isolated vertices added.

Note: Depending on the current default graph product (check DefaultGraphProduct[]), this command is equivalent to g+k.


AddDominatingVertex[g]
AddDominatingVertex[g,k]

This returns the graph object g with a dominating vertex added, or if the optional argument k is given, then it returns the graph with k dominating vertices added.


AddIsolatedLoopedVertex[g]
AddIsolatedLoopedVertex[g,k]

This returns the graph object g plus an isolated vertex with a loop, or if the optional argument k is given, then it returns the graph with k isolated vertices with loops added.

Note: Depending on the current default graph product (check DefaultGraphProduct[])), this command is equivalent to g+k.


AddLoops[g]
AddLoops[g,{v1,...}]

This returns the graph object g with loops added to each vertex, or if the optional list of vertices is given, it returns g with a loop added only to those vertices in the list.


AddPendents[g]
AddPendents[g,{v1,...}]

This returns the graph object g with pendents added to each vertex, or if the optional list of vertices is given, it returns g with a pendent added only to those vertices in the list.


RyserSwitch[g,u,v,x,y]

This function performs a Ryser switch on the edges uv, xy in the graph object g.

Note: Given a graph g and four vertices u, v, x, y such that:

  1. all of u, v, x, y are distinct,
  2. uv, xy are edges in g,
  3. ux, vy are not edges in g,
the Ryser switch on uv, xy in g replaces the edges uv and xy with the edges ux and vy.


PartiteSets[g]

Given a bipartite graph g, this function returns a pair {A, B} of partite sets, i.e., a bipartition of the vertex set V(g) such that all the edges in g go from A to B.

Warning: These are only uniquely determined if g is connected.


KeepNonIsomorphic[{g1,...}]

Given a list of graphs, this returns a list with any isomorphic duplicates removed.


Nullity[g]
Nullity[m]

Even though the nullity of a matrix m (or graph g) is a standard concept in linear algebra (i.e., the dimension of its nullspace), there is no Nullity[] function in Mathematica by default, so we provide one here.


CartesianProduct[g,h]

This gives the Cartesian product of g and h.
By default, this can also be done just by doing g h.


DirectProduct[g,h]

This gives the Direct product of g and h.

Note: If you run DefaultGraphProduct["Direct"], then subsequently the direct product is just g h.


StrongProduct[g,h]

This gives the Strong product of g and h.

Note: If you run DefaultGraphProduct["Strong"], then subsequently the strong product is just g h.


LexicographicProduct[g,h]

This gives the Lexicographic product of g and h.


DefaultGraphProduct[]
DefaultGraphProduct["product"]

This displays on screen the definition of juxtaposition for graph objects, i.e., the meaning of the product g h for graph objects g and h (and by extension, other algebraic expressions such as g2+1).
DefaultGraphProduct["product"] sets the meaning of the product g h for graph objects g and h to the specified product.

Note: Options for "product" include "Cartesian", "Direct" and "Strong".


SeidelSwitch[g,U]

This performs a Seidel switch on the graph g with respect to the subset U of the vertex set.

Note: Given a graph g and a subset U ⊆ V(g), the Seidel Switch interchanges all edges between U and V(g)∖U in g.


DescendantForm[g]
DescendantForm[g,v]

This gives a graph obtained from g by Seidel switching a certain subset which guarantees the presence of an isolated vertex.
The optional argument v is the vertex which ends up being isolated after the Seidel switch.

Note: If you take the set U to be the set of neighbours of the vertex, then you isolate that vertex when Seidel switching.


SeidelMatrix[g]

This gives the Seidel matrix representation, i.e., the (0,1,-1)-adjacency matrix of the graph g.


SeidelGraph[m]

This converts a given Seidel matrix into the corresponding graph object.


VertexDrag[g]

This returns the graph object g, with vertices which can be clicked and dragged.


AntipodalVertices[g]

This returns a list of all the pairs of vertices in the graph object g which are antipodal, i.e., as far from each other as possible.

Uninstalling the Package

To uninstall the package, you just need to delete the file Walks.wl from the place where Mathematica placed it when it was first installed. Usually, it's one of the directories outputted by these commands:

Click on code to copy to clipboard
Locate package directory

You can open either directory using your default file explorer program by running

Click on code to copy to clipboard
Open package directory

(for instance), and then just deleting the file Walks.wl. If you don't find the file in either of those places, make sure it's not in the same directory as the current notebook you're working in, cause Mathematica would look there for packages too. Failing that, you can run:

Click on code to copy to clipboard
Find package file

The above command searches all of directories in Mathematica's $Path variable, which is where it usually looks for package files. You can then delete it by doing:

Click on code to copy to clipboard
Delete found package file

Or if, for some reason, you don't like Mathematica deleting files for you, you can open the directory by doing:

Click on code to copy to clipboard
Open directory of found package file

and delete the file manually yourself.