Talks
The Canonical Double Cover of a Graph
30th March, 2023
This is a talk I gave at the GCGN2023 conference organised by the Mathematics Department at the University of Malta. I presented some of the research I was doing together with Prof. Irene Sciriha on 2–1 projections, and CDCs of simple graphs.
A (Gentle) Introduction to Number Theory
29–31st August, 2022
In this three-part lecture series for the Malta Mathematical Society, I first went over some basic arithmetical functions (μ, φ and Λ) and their properties, used partial summation to prove Chebychev's theorem, and discussed how to prove the Prime Number Theorem. Next, I discussed modular arithmetic, some applications, and explained how to implement Diffie-Hellman key exchange, as well as RSA encryption with Python.
PDF Notes (Lecture 1 Only)

Inter-blockchain Communication (IBC)
21st February, 2022
This is a talk I gave to the research team at Simply-VC, where I went over the lifecycle of a packet being sent over IBC: a protocol designed by the Interchain Foundation to allow autonomous blockchains to communicate with each other. I also went over the corresponding Cosmos-SDK Module.

Finding Holes: Homology and Cohomology
20th September, 2021
This is a talk I gave for the Malta Mathematical Society as part of the Differential Geometry Lecture Series. First I gave an informal introduction to the ideas of homology and cohomology, as two different strategies for identifying holes in manifolds. Subsequently, I described de Rham's theorem, showing that homology and cohomology measure the same "holes", and Stoke's theorem, the higher dimensional analogue to the fundamental theorem of calculus.

Eigenvalues in Number Theory: Ramanujan Graphs
29th April, 2021
29th April is "Eigenvalue Day", and so the Malta Mathematical Society organised a series of talks on eigenvalues. For the occasion, I gave a talk on a use of eigenvalues in number theory—in particular, I described the use of the second largest eigenvalue as a measure of connectivity in a graph, the idea of Ramanujan graphs, and why they make good expanders.
Elementary Number Theory: Quadratic Reciprocity
22nd April, 2021
Quadratic Reciprocity is one of the most important theorems in all of mathematics. In this talk for the Malta Mathematical Society, I motivated quadratic reciprocity by introducing modular arithmetic and finite fields. I subsequently computed some Legendre symbols using the result.
Debate: Is Mathematics Invented or Discovered?
5th March, 2021
The Malta Mathematical Society organised a debate on the age-old question of whether mathematics is invented or discovered. I was on the "invented" side of the argument, and we won the debate by changing the most votes from audience members.
Factorials of Large Numbers
18th November, 2020
In this talk, I introduced the idea underlying the technique of partial summation which is often applied in analytic number theoryto obtain asymptotic bounds for sums by expressing them in terms of integrals. Using this technique and its more general form (the Euler–Maclaurin formula), one can obtain Stirling's approximation for factorials. I gave an estimate of 10000! using this approximation; and ended by discussing the de Polignac formula for factors of N!.
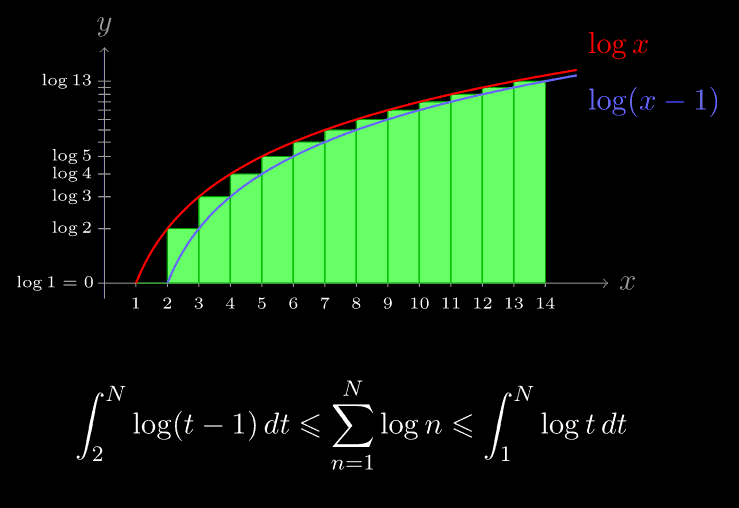
Smooth Submanifolds
6th July, 2020
As part of a Differential Geometry reading group at the University of Warwick Mathematics Institute, I gave a talk on chapter 5 of Lee's book on Smooth Manifolds, about smooth submanifolds. The talk comprises embedded submanifolds, immersed submanifolds, and the tangent space to a submanifold.
The Lambda Calculus
18th December, 2019
I gave a lecture on Church's \(\lambda\)-calculus (Lambda calculus). The \(\lambda\)-calculus is a very simple formal language which is expressive enough to serve as a foundation for mathematical logic. In the talk, I discussed what a formal language is, explored some of the history of mathematical logic and finally demonstrated how the \(\lambda\)-calculus can model various mathematical structures. The \(\bf Y\)-combinator was also mentioned briefly.

Synthesising Runtime Enforcement Monitors for \(\boldsymbol\mu\textbf{HML}\)
10th June, 2019
This talk is on my undergraduate computer science dissertation. I considered a subset \(\text{sHML}\) of formulæ in the Hennessy-Milner Logic with recursion (\(\mu\text{HML}\)) which are enforceable through suppressions. A synthesis function is introduced, which converts safety properties in \(\text{sHML}\) to suppression enforcers through a formula normalisation process.

Walks and CDCs of Comain Graphs
12th April, 2019
The S³ Science Conference is an event organised by the Faculty of Science students' society, as an opportunity for students of the faculty to present their work to their fellow students. In 2019, the event was held at Esplora, a science museum in the south of Malta. I presented research related to a publication I coauthored with my undergraduate mathematics dissertation supervisor, Prof. Irene Sciriha.
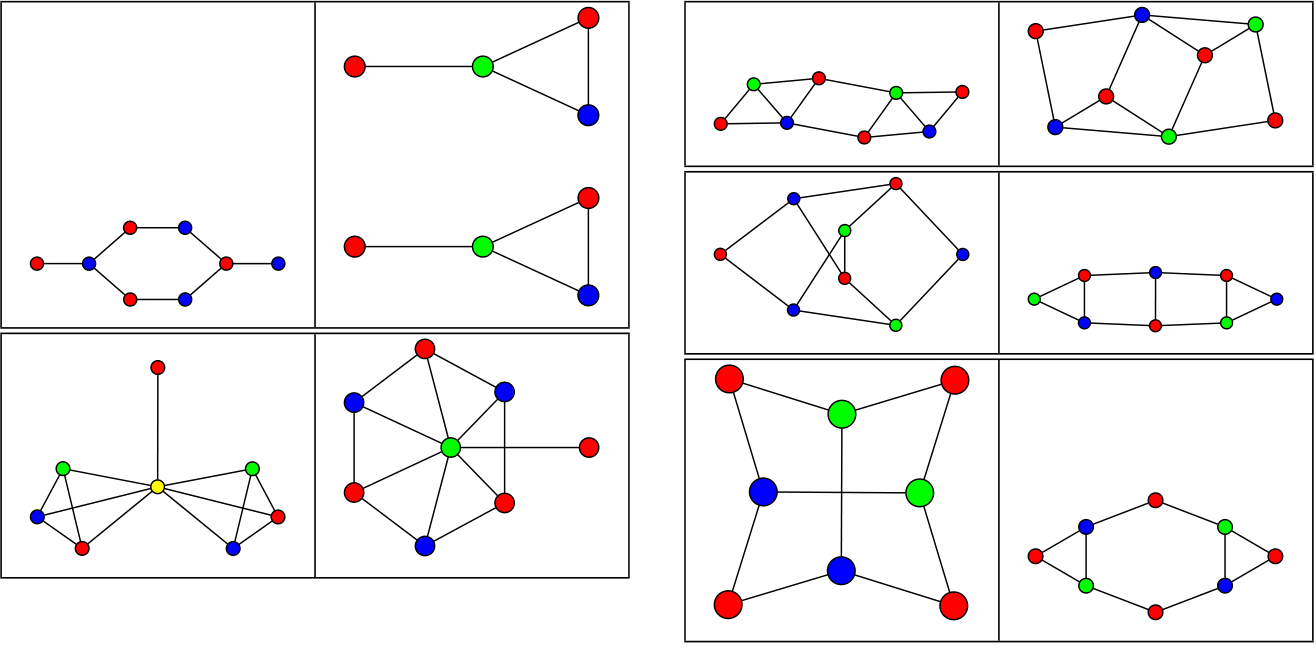
Two-Graphs and Conference Graphs
31st January, 2019
The Combinatorics and Graph Theory Day was an event organised by the Department of Mathematics at the University of Malta, where research was presented by researchers from the department, as well as researchers from the Mathematics Department of the University of Pannoia, Hungary. I presented research I conducted on two-graphs and conference graphs as an undergraduate student.
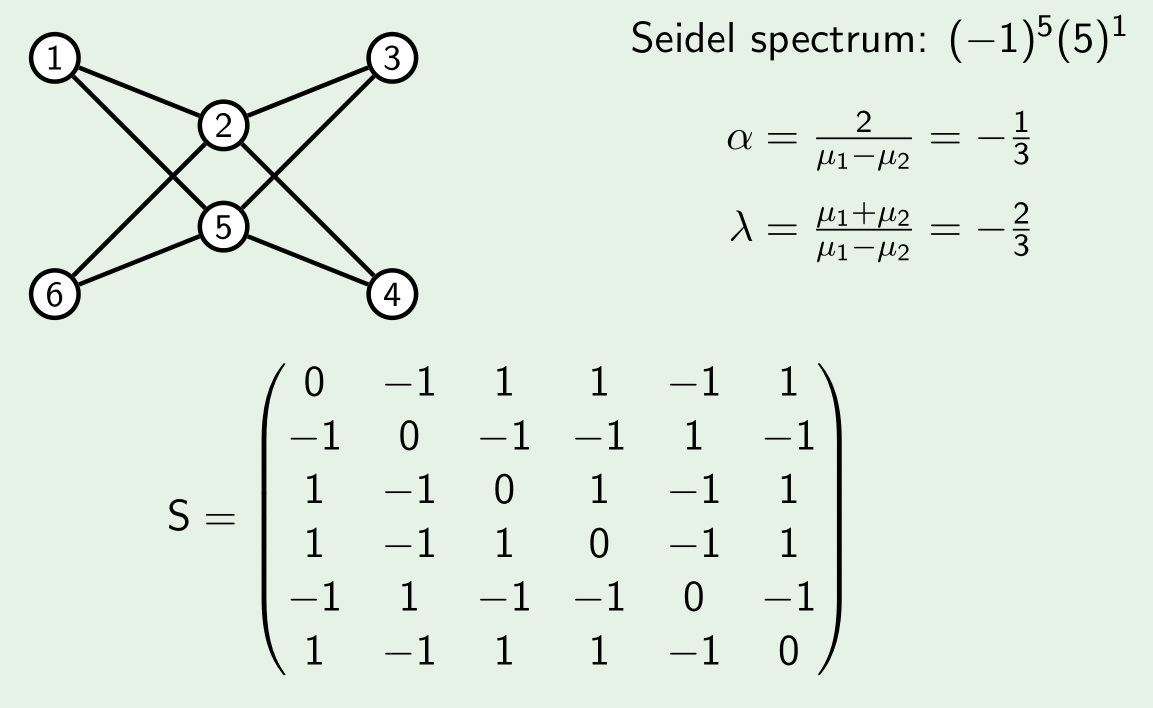
Two-Graphs and NSSDs: An Algebraic Approach
2nd March, 2018
The S³ Science Conference is an event organised by the Faculty of Science students' society, as an opportunity for students of the faculty to present their work to their fellow students. I presented research I conducted on two-graphs and non-sigular graphs with a singular deck (NSSDs).